|
½Оптимизация
алгоритмов идентификации графового изоморфизма╗
½Optimization
of graph isomorphism identification algorithms╗
С.В. Москаленко, Ю.А. Гатчин ¢ д.т.н.
В статье
авторами предложен ряд оптимизирующих моментов для
современных алгоритмов идентификации графового изоморфизма,
призванных увеличить скорость работы данных алгоритмов с
сохранением точности вычисления результатов.
Ключевые слова:
теория графов, распознавание графических образов,
определение межграфового изоморфизма.
Введение
В последнее время наблюдается рост
необходимости в обработке больших объемов инженерной
документации, в частности приборостроительные и
машиностроительные чертежи. Эта тенденция возникла в связи с
активизацией использования электронной версии инженерной
документации в САПР [1]. Довольно частой практикой для
инженеров и проектировщиков является обращение к уже
существующей документации, однако данный процесс всегда
оказывается трудоемким, т.к. требуется просмотр всей базы
данных чертежей. Для упрощения данного поиска часто
используется текстовая составляющая документа, когда
происходит просмотр по ключевым словам. Данный подход весьма
эффективен, но существуют трудности связанные с получением
этой текстовой информации (необходимо вмешательство человека),
кроме того, набор ключевых слов не всегда точно может
описать содержание чертежа. Поиск требуемого изображения в
БД есть не что иное, как проблема сопоставления графических
объектов, которая может быть решена путем вычисления степени
соответствия входного объекта объекту в базе данных (БД) и
сведена к процессу сопоставления графов. Для этого
инженерная документация сначала приводится к представлению
атрибутивных графов, где вершины графов отображают примитивы,
полученные из исходных документов (линии, кривые) [2], а
топологические связи между этими примитивами описаны ребрами
графов. Далее вершины графов задаются метками, которые
вычисляются по некоторой функции. Метки, как правило,
являются целыми числами и используются для сравнения входных
графов с заданными в БД графами. Таким образом, сравнивая
ребра и метки графов, чертежи, находящиеся в БД, целиком или
частично схожие с текущим чертежом, могут быть обнаружены.
В данной статье внимание обращено
на подкласс процесса сопоставления графов ¢ на проверку
графов на изоморфизм (далее графовый изоморфизм или ГИ).
Проблему идентификации ГИ можно определить: два графа G=(V1,
E1) и H=(V2, E2)
изоморфны, если между парами множеств их вершин, ребер и дуг
существуют взаимно однозначные соответствия, сохраняющие
смежность и ориентацию для дуг (см. определение 1).
Будучи полезным в различных
направлениях современной жизни: определение поврежденных
клеток на медицинских снимках, поиск изоморфных химических
соединений [3], сравнение пар кинематических цепей [4], и
т.д.; для решения проблемы поиска ГИ, однако, не существует
достаточно эффективных алгоритмов, обладающих полиномиальным
временем исполнения, даже если алгоритм ограничен по области
применения (например, операции проходят над строго
однородными графами). В работе [5] представлен эффективный
алгоритм, обладающий сложностью вычисления
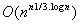 , но оперирующий лишь со строго однородными графами. В работе [6]
приведен еще один алгоритм, являющийся линейным для
большинства случайных графов. Однако последний имеет ряд
недостатков, которые связаны с невозможностью разрешения
неопределенных ситуаций, возникающих при обнаружении
множества идентичных друг другу вершин (см. определение 2).
В рамках данной работы предложены 3 оптимизационных момента,
призванные ускорить поиск ГИ в современных алгоритмах
сопоставления графов. , но оперирующий лишь со строго однородными графами. В работе [6]
приведен еще один алгоритм, являющийся линейным для
большинства случайных графов. Однако последний имеет ряд
недостатков, которые связаны с невозможностью разрешения
неопределенных ситуаций, возникающих при обнаружении
множества идентичных друг другу вершин (см. определение 2).
В рамках данной работы предложены 3 оптимизационных момента,
призванные ускорить поиск ГИ в современных алгоритмах
сопоставления графов.
Реализация алгоритма
В данной главе сформулирован
обобщенный алгоритм работы многих современных систем
идентификации ГИ [6, 7]. На старте алгоритм имеет некоторый
входной помеченный граф (вершинам которого приписаны метки),
а также база данных эталонных помеченных графов. Требуется
найти граф в БД изоморфный входному графу (см. определение
1). Сперва алгоритм строит связи между всеми вершинами
входного графа со всеми вершинами эталонного графа в БД,
которые имеют одинаковые метки. Ситуацию, когда одна вершина
в одном графе идентична (см. определение 2) с несколькими
вершинами в другом, называют неопределенной. На следующих
шагах после обнаружения удовлетворяющего эталона, алгоритм
пытается сократить число ложных связей. Для снижения числа
случаев ошибочного определения изоморфизма отдельные
алгоритмы, например [6], реализуют вовлечение информации о
соседних вершинах в функцию вычисления меток.
Итак, обобщенный алгоритм
идентификации ГИ выглядит следующим образом:
Ę
Шаг 1 (Предобработка):
Первым делом для входного графа и для всех графов в БД
высчитываются степени у вершин, и собирается другая
необходимая для последующих шагов информация, например, тип
линии для примитивов инженерных чертежей. Далее полученные
данные используются в качестве аргументов функции вычисления
меток. Вдобавок, на данном шаге также может собираться
информация о соседних вершинах (количество степеней и пр.)
для включения в функцию вычисления меток.
Ę
Шаг 2 (Построение
связей): Связи строятся между двумя сравниваемыми графами
для всех пар вершин, которые имеют одинаковые метки. Пример
таких связей приведен на рисунке 1, где различные метки
показаны черным, белым или серым цветом, вершина u графа G связана
с вершиной v графа Н.
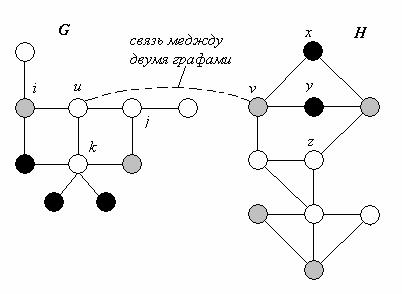
Рис. 1. Построение связи между двумя графами
Две вершины соединены потому, что
метка от u совпадает с меткой от v, т.е. метка
и степень вершины u равны соответствующим значениям
вершины v, а также каждый потомок (смежная вершина)
от узла u, а именно i, j, k, имеют
соответствующего потомка от узла v с такой же меткой
и степенью. На рисунке 1, потомки i, j, k графа G совпадают
с x, y, z на графе H соответственно. Однако
ясно видно, что графы G и H не изоморфны.
Ę
Шаг 3 (Редукция
энтропии): Данный шаг является самой затратной частью
алгоритма, исходя из аспекта количества вычислений.
Происходит попытка разрешить неопределенные ситуации, если
таковые возникли на предыдущем шаге, и сделать вывод о
наличии изоморфизма между входным графом и эталонным графом.
На рисунке 2 изображены все шаги
представленного алгоритма. На этапе предобработки (рис. 2,
а) для обоих графов вычисляются метки для каждой вершины.
Здесь каждая вершина содержит метку с информацией о текущем
узле, а также о его соседях. Вдобавок следует отметить, что
все метки графов G и Н одинаковы
как внутри графов, так и между G и Н.
Это равенство обусловлено тем, что метки самих вершин
изначально равны (все кружочки отмечены белым цветом), оба
графа являются однородными (одинаковое число ребер смежных с
каждым узлом). Данное равенство дает высокую степень
неопределенности (см. определение 3), когда каждая вершина
графа G может
быть соединена с каждой вершиной Н (рис.
2, б). Неопределенность разрешается на шаге редукции
энтропии (рис. 2, в), когда стартует детальный анализ графов.

Рис. 2.
Иллюстрация работы алгоритма поиска ГИ: а - шаг
предобработки, даны 2 графа
G
и Н; б ¢ шаг построения связей; в ¢ шаг редукции
энтропии
Оптимизационные меры
В предыдущей главе был показан
пример (рис. 2), когда при сопоставлении двух графов
возникали избыточные неопределенные ситуации. Разрешение
таких ситуаций ¢ весьма трудоемкий процесс, требующий
вовлечение процедуры детального анализа графов, во время
работы которой происходит последовательное продвижение по
уровням графа (каждый уровень характеризуется набором всех
вершин смежных с любой текущей вершиной). Также существует
еще ряд проблем, опять же связанных с трудозатратами,
которые линейно возрастают по мере добавления в БД эталонных
графов. Для разрешения этих вопросов в данной главе
приведены два критерия и один момент, которые могут быть
вовлечены в любой алгоритм поиска ГИ в качестве
оптимизирующих мер.
Ниже даны несколько ключевых
определений.
Определение 1.
Графовый изоморфизм.
Даны 2 графа G=(V1,
E1) и H=(V2, E2),
где │V1│=│V2│.
Граф
G
изоморфен Н (G=Н),
при V1 →V2 │
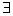 (u,
v) E1 && (u,
v) E1 &&
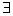 (f(u),
f(v)) (f(u),
f(v))
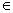 E2
&& l(u) E2
&& l(u)
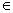 l(f(u))│ l(f(u))│
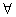 u u
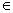 V1.
Где l
¢ функция вычисления метки для вершины. V1.
Где l
¢ функция вычисления метки для вершины.
Определение 2.
Соответствие (идентичность) вершин. Пусть
u
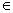 V1
вершина графа
G,
а
v V1
вершина графа
G,
а
v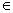 V2
вершина графа Н. Считается, что узел
u
идентичен узлу
v,
если метка от
u
равна метке от
v. V2
вершина графа Н. Считается, что узел
u
идентичен узлу
v,
если метка от
u
равна метке от
v.
Определение 3.
Степень неопределенности узла
u,
принадлежащего графу
G, называется число узлов графа Н, с которыми
u идентичен. Существует обозначение
deg(u)=m,
где m
¢ число вершин 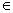 Н,
которым соответствует узел
u. Н,
которым соответствует узел
u.
Критерий
1.
При поиске эталонного графа в БД изоморфного входному, для
каждого графа в БД запускается алгоритм идентификации ГИ,
описанный выше. Ясно, что это весьма трудоемкий подход,
требующий большого количества вычислений. Для оптимизации
поиска ГИ можно ввести условие, что во время первого пробега
(последовательного сопоставления входного графа с каждым
эталонным) алгоритм идентификации ГИ должен запускаться лишь
для эталонных графов с числом вершин равным или меньшим
числа вершин входного графа. Данное условие применимо лишь
для графов, которые отражают графическую информацию,
заложенную на изображениях (инженерная документация, чертежи).
Для таких изображений характерно наличие шумов,
сказывающихся появлением на графах дополнительных вершин и
ребер. Действительно, при разрыве линии на чертеже или, при
появлении случайного штриха, вызванного недостатками
процесса сканирования, появляются шумы, которые, однако, не
повлияют на вывод о наличии ГИ.
На вход процедуры сравнения
графов подается (G
¢ входной граф, {Н} ¢ множество эталонных графов в БД,
G=(V1,
E1) и H=(V2, E2))
1.
Для каждого Н
2.
если (│V1│≥│V2│)
3.
выполняется
алгоритм поиска ГИ
4.
если (ГИ обнаружен)
5.
тогда выход их
программы
с результатом ½ГИ
найден╗
6.
Для каждого Н
7.
если (│V1│<│V2│)
8.
выполняется
алгоритм поиска ГИ
9.
если (ГИ обнаружен)
10.
тогда выход их
программы
с результатом ½ГИ
найден╗
11.
Выход из программы с результатом ½ГИ не найден╗
Критерий 2.
Также, при поиске эталонного графа в БД изоморфного входному,
можно добавить еще одно условие запуска алгоритма
идентификации ГИ. Данный запуск должен происходить лишь
тогда, когда набор меток входного графа равен набору меток
эталонного. Здесь под равенством понимается, что для каждого
элемента набора эталонного графа существует идентичный
элемент набора входного графа (набор ¢ есть совокупность
уникальных внутри данной совокупности элементов).
G=(V1,
E1) ¢ входной граф,
H=(V2,
E2) ¢ эталонный граф, {Н}
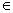 БД. БД.
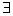 набор
меток F1,
заданных функцией
l(u)→
F1, набор
меток F1,
заданных функцией
l(u)→
F1,
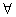 u u
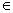 V1 V1
&
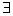 набор
меток F2,
l(v)→
F2, набор
меток F2,
l(v)→
F2,
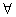 v v
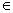 V2 V2
→{
l(u)}
≥ { l(v)}
Количество элементов набора
входного графа может быть больше или равно количеству
элементов эталонного. Данное допущение основано на природе
графических изображений, получение которых может
сопровождаться шумами (см. также критерий 1),
обуславливающими увеличение числа вершин и ребер
соответствующего графа.
1. Для каждого Н
2. если
({ l(u)}
≥ { l(v)})
3.
выполняется алгоритм поиска ГИ
4. если (ГИ
обнаружен)
5. тогда выход их
программы
с результатом ½ГИ найден╗
6. Для каждого Н
7.
если
({ l(u)}
< { l(v)})
8. выполняется
алгоритм поиска ГИ
9. если
(ГИ обнаружен)
10.
тогда выход их программы
с
результатом ½ГИ найден╗
11.
Выход из программы с результатом ½ГИ не найден╗
Оптимизационный момент.
Еще один момент может быть применен непосредственно в самом
алгоритме идентификации ГИ. Суть момента заключена в
предложении того, что на шаге предобработки графов, когда
вычисляются степени для вершин, все узлы со степенью 2
должны быть удалены, а соответствующие две вершины смежные с
только что удаленным узлом объединены в одну. Во время
объединения двух вершин происходит формирование новой метки,
связанной с новым узлом, которая хранит атрибуты удаленной
вершины.
На рисунке 3 представлен пример
работы данного момента. Дан фрагмент инженерного чертежа (рис.
3, а), разбитого на примитивы, каждому из которых приписан
свой порядковый номер. Далее происходит переход к графовому
представлению чертежа (рис. 3, б). Проанализировав последнее
представление, можно сделать вывод о наличии избыточных
узлов (узел 4, со степенью равной 2), которые можно удалить,
объединив две смежные вершины 3 и 5 в одну (рис. 3, в).
Использование данной
оптимизационной меры сокращает количество узлов в графах,
что повышает скорость работы алгоритма, при этом степень
информативности графов не снижается. Вдобавок метки
приобретают более содержательный характер, что снижает
степень неопределенности (см.
определение 3).
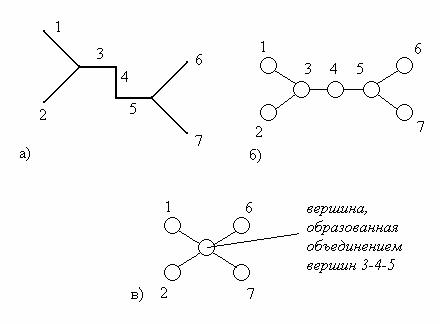
Рис. 3.
Пример работы оптимизационного момента: а ¢ входной чертеж с
пронумерованными примитивами; б ¢ графовое отображение
чертежа; в ¢ объединение вершин графа
Заключение
В статье авторами разработаны и
представлены оптимизационные меры (два критерия и один
момент), которые могут быть включены в любой современный
алгоритм поиска изоморфизма среди графов. Данные меры не
снижают точность работы данных алгоритмов, и в то же время
являются весьма надежными.
Первые два критерия вовлекаются в
процесс сопоставления входного графа с эталонными графами в
БД. Здесь на ранних стадиях сопоставления происходит
сравнение вершин и меток, пропуская тем самым
неудовлетворяющие критериям графы без их последующего
детального анализа, что приводит к росту производительности
системы. Оптимизационный же момент должен быть применен
непосредственно в самом алгоритме идентификации ГИ, снижая
степень неопределенности графов и повышая информативность
меток, что дает более быструю и точную работу процедуры
сопоставления графов.
В дальнейших работах планируется
реализация данных оптимизационных мер на языке
программирования и проведение нагрузочного тестирования для
исследования изменения производительности алгоритмов поиска
ГИ.
Литература
1. Tombre, K.: Analysis of engineering
drawings: state of the art and challenges. In Graphics
recognition - Algorithms and systems, volume 1389 of Lecture
Notes in Computer Science, Springer-Verlag 1998; 257-264.
2. Москаленко С.В., Гатчин Ю.А.
Волновой алгоритм векторизации линейных растровых
изображений // Научно-технический вестник СПбГУ ИТМО. ¢
2008. №51.
3. Xu J.: A
Generic Match Algorithm for structural homomorphism,
isomorphism, and maximal common substructure match and its
applications. J Chem Infor Comput Sci 1996; 36(1): 25-34.
4. Rao A.C., Varada Raju D.: Application
of the Hamming number technique to detect isomorphism among
kinematic chains and inversions. Mech Mach Theory 1991;
26(1): 55-75.
5. Spielman D.A.: Faster isomorphism
testing of strongly regular graphs. Technical report,
University of California Berkeley, Computer Science
Division, Berkeley, California, 1996.
6.
Abdulrahim M.,
Misra M.:
A Graph Isomorphism Algorithm for Object. Recognition,
Pattern Analysis and Applic. 1998; vol. 1, no. 3: 189-201.
7. von der Malsburg C, Bienenstock E. A.:
neural network for retrieval of superimposed connection
patterns. Europhysics Let 1987; 3(11): 1243-1249.
go to published works page ->
|