Moskalenko Stanislav's Personal Page

Published works

�Алгоритм вычисления пороговых значений для повышения автоматизма систем распознавания графических образов�

С.В. Москаленко, Ю.А. Гатчин � д.т.н.

Санкт-Петербургский государственный университет информационных технологий, механики и оптики, г. Санкт-Петербург.

В данной статье представлена система идентификации линейных объектов на инженерных чертежах. По завершении работы данная система использует полученный набор данных для определения различных пороговых значений необходимых для автоматизации алгоритмов анализа изображения, таких как векторизация.

This article represents the algorithm that is used to identify all linear objects in the engineer drawings. After finishing its work the algorithm uses extracted data set to compute different thresholds that are typically entered by human in different image analysis systems. In this way the automation of such systems increases.

Введение

Сегментация � одна из ключевых открытых проблем в компьютерном зрении. До недавнего времени распознавание и сегментацию не связывали вместе. Однако в области сегментированного представления мало таких тем, изучение которых не помогло бы решить задачи, связанные с распознаванием [1].

Большинству систем распознавания графических изображений, на вход подается некоторый избыточный набор неструктурированных данных. После чего система должна отсеять лишнюю информацию и выделить множество с интересующими характеристиками. Данный процесс получения компактного представления полезного содержимого объекта и называется сегментацией или идентификацией. Верное выявление важной информации на изображениях обеспечивает надежное функционирование систем распознавания образов, а также является базисом для систем восстановления изображений. На практике, проблема сегментации изображений является довольно трудноразрешимой.

Как правило, многие системы распознавания графических изображений включают процедуру сегментации в этап первичной векторизации, во время которого происходит конвертирование пиксельного набора изображения в векторное представление [2]. В контексте этапа векторизации сегментация занимается не только поиском информативных графических примитивов, но и подразделением совокупностей данных примитивов на простейшие группы. В частности, множество примитивов включает: точки, векторы, объединение которых может быть определено как текст или графика, площадной объект или линейный. Процедура сегментации в таких системах часто нуждается в определении специальных пороговых значений, которые задаются в диалоговом режиме оператором [3, 4, 5]. Так, применимо к задаче анализа инженерных чертежей почти всегда требуется, чтобы пользователь задал такие пороги: ширина линии, максимальная длина луча для определения ширины объекта, расстояние между штрихами, основываясь на которых система судит о типе конкретного линейного объекта: основная или тонкая линия, штрих пунктирная линия или разрыв объекта из-за помех на растре.

В большинстве случаев данные пороговые значения определяются эмпирическим путем, что лишает систему автоматизма. Поэтому разработка автоматизированных методов вычисления пороговых значений остается актуальной. В данной статье предложен автоматический алгоритм, вычисляющий ширину основной и тонкой линии на изображении, отталкиваясь от которых возможно определение других порогов.

Реализация алгоритма

Разработанный алгоритм сегментации должен отделять линейные объекты от площадных и дискретных объектов. Примерно 90% объектов на инженерных чертежах составляют линии. Исходя из ГОСТ 2.303-68 единой системы конструкторской документации, все эти линии могут быть разделены на 2 группы по признаку ширины: основные (сплошная толстая основная линия), тонкие (сплошная тонкая, сплошная волнистая, штрихпунктирная тонкая линия). Суть алгоритма заключена в идентификации любых линейных объектов на изображении, поэтому изначально алгоритм не будет знать, к какой группе отнести обнаруженный линейный объект: данный объект может принадлежать либо группе основных линий, либо тонких, либо вообще оказаться площадным объектом (площадной объект может обладать характерными атрибутами линейного, когда длина значительно больше ширины). Замеряя ширину найденных линий, алгоритм формирует выборку, исходя из которой, вычисляется среднее арифметическое ширины линии для каждой группы. Полученная информация о ширине линейных объектов поможет на следующих этапах анализа изображения отделять линейные объекты от площадных объектов,  определять пороговые значения в автоматическом режиме и вычислять точки центральной линии.

Работа алгоритма начинается с введения в систему бинарного чертежа. Далее происходит наложение сетки на введенное изображение, тем самым происходит обнаружение точек (пикселей) лежащих на границе графических примитивов с фоном. Данный процесс представляет собой сначала горизонтальное, а потом вертикальное сканирование изображения на наличие черных точек, говорящих о встрече некоего объекта. Что касается выбора интервала между штрихами скан-линий, то здесь можно задать строгое соответствие разрешения изображения к интервалу между штрихами. Например, опытная эксплуатация показала, что при размере изображения 1600 на 1200 пикселей и интервалом в 10 пикселей алгоритм будет обладать оптимальным соотношением скорости работы к точности вычисления ширин линейных объектов. 

После обнаружения некоторого объекта от полученной исходной точки в основных направлениях строится циклическая гистограмма, замеряющая ширину объекта в каждом из направлений, осуществляется проход  по черным пикселям до первого белого. Направления измерения ширины можно последовательно проводить по часовой стрелке с приращением угла α, начиная от луча, совпадающего со сканирующей линией, обнаружившей данный объект. В связи с недостаточно высоким  разрешением изображения и с ограниченным числом лучей циклической гистограммы, длина участка пересечения лучом графического объекта может отличаться от реальной толщины объекта в данной точке. Ошибка вычисления толщины для такого случая определяется по формуле (1):

Δ =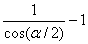,                                              (1)

где α � угол между смежными лучами.

Число лучей гистограммы может быть взято равным 18, так как при α = 10 градусов ошибка вычисления толщины объекта не превысит 1,5%.

Для построения гистограммы ширина объекта в каждом из направлений рассчитывается типовым алгоритмом Брезенхема [6]. В результате  могут получиться гистограммы  с ярко выраженными или неопределенными пиками. Гистограммы в большинстве случаев будут иметь гладкий непрерывный вид (рис. 1, а), однако в некоторых случаях, когда исходный растр достаточно зашумлен и имеет �дыры� в объектах, график будет терять свою гладкость (рис. 1, б). Для повышения точности определения типа объекта и повышения точности вычисления его ширины необходимо для зашумленных изображений сглаживать гистограммы. Это можно сделать путем вычисления в каждой точке графика усредненного значения, принимая во внимание значения соседних точек.

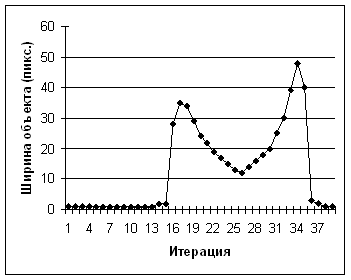
Рис. 1. Примеры гистограмм растровых изображений

(слева растровое изображение, справа гистограмма): а � гладкая; б � возмущенная

 Под ярко выраженным пиком понимается участок на графике, когда функция резко возрастает в один момент и далее резко убывает.  Под впадиной понимается точка экстремума на графике, когда функция резко убывает в один момент и далее резко возрастает. Будем считать любой объект, одно из измерений которого больше измерения другого в 4 раза линейным (длина в 4 раза больше ширины). Следовательно, для такого объекта на графике должно существовать два явных пика с высотами минимум в два раза большими, чем величина впадины между ними (рис. 2). Исходя из данного положения, можно сформулировать метод, проверяющий является ли текущий объект линейным. Для начала полученную гистограммную развертку следует минимизировать, сформировав тем самым массив экстремальных точек. Данная мера является чисто оптимизационным моментом, так как для анализа графика достаточно лишь информации об экстремумах. Далее находим экстремум у_мах, принадлежащий самому высокому пику (рис. 3, а). Отталкиваясь от у_мах можно однозначно заключить, что если за данным пиком следует впадина с у_впад < у_мах / 2, а за впадиной находится пик с у_пик > у_впад * 2, то рассматриваемый объект � линия. Для проверки данных условий, надо исследовать c какими отрезками, последовательно соединяющими точки экстремума, пересекается линия f = у_мах / 2 (рис. 3, а). Если линия f пересечет два пика, значит идентифицируемый объект линейный, и теперь остается только проверить график между этими двумя пиками на непрерывность и найти на данном интервале минимальную впадину с у_мин > 2 пикселя. у_мин будет являться искомой шириной линии.

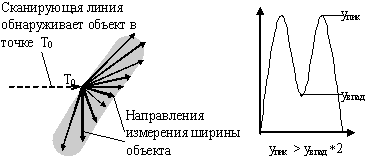
Рис. 2. Упрощенный вид линейного объекта (слева), его гистограмма (справа)

Однако есть вероятность, что при построении линии f будет найден лишь один пик, хотя идентифицируемый объект будет линейным (рис. 3, б). Для таких случаев существует ответвление алгоритма. Происходит запуск перебора массива экстремумов вначале в одном направлении и, если не обнаружен второй явный пик, характеризующий конец линии, в другом. Во время этого перебора происходит проверка: если для текущего пика существует такое  у_в, что у_п > 2*у_в, значит обнаружен второй явный пик, и далее идет поиск минимальной впадины у_мин между этими двумя пиками,  выход из текущей итерации попиксельного сканирования и запуск следующей итерации.

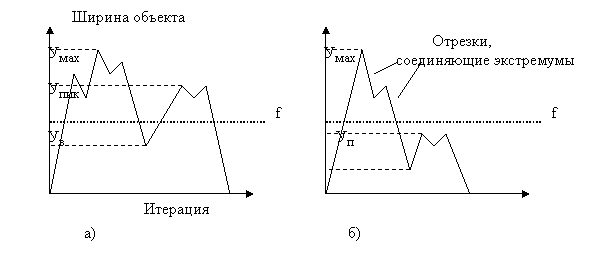
Рис. 3. Схемы экстремумов для линейных объектов: а � обнаружено два явных пика; б � обнаружен один явный пик

Таким образом, по окончании операции поиска линейных объектов, алгоритм будет обладать статистической выборкой, содержащей ширины всех найденных линий. Как было сказано, все линейные объекты можно грубо отнести к группе основных или тонких линий, значит каждая выборка должна иметь две преобладающие величины, где меньшая величина соответствует усредненной ширине тонкой линии, а большая � ширине основной линии.

Заключение

Разработанный алгоритм, предназначенный для анализа графических данных, дает на выходе две важные величины: ширина основной и ширина тонкой линии. Далее отталкиваясь от этих двух значений можно сконструировать основные пороговые значения, которые задаются в современных системах распознавания образов и обработки изображений человеком. Таким образом, данный алгоритм автоматизирует работу систем на более высоких уровнях.

Так как данный алгоритм должен применяться в системах в качестве дополнительного уровня предобработки, значит принципиальным остается вопрос о скорости его работы. Большое внимание было уделено его оптимизации. В частности реализован разреженный просмотр растра: наложение сетки на изображение вместо попиксельного сканирования, ограниченное число направлений измерения ширины объекта для построения гистограммы. Вообще лучший результат алгоритм показал при анализе отсканированного чертежа формата А4 с 600dpi (разрешение 3350 на 5694 пикселей). Реализация алгоритма была написана в среде разработки Borland Delphi 7. На компьютере средней конфигурации Celeron 1,7 Ghz с 512 Mb оперативной памяти расчет проходил около 1 секунды вместе с точным выявлением ширин линий. Если реализовать данный алгоритм на более низкоуровневом языке программирования, то скорость работы увеличится в разы.

Точное и быстрое определение пороговых значений является важным этапом  в системах обработки изображений. От этих значений будут зависеть процедуры анализа изображения более высокого уровня, такие как распознавание графических образов в САПР. Разработанный алгоритм обладает всеми необходимыми характеристиками для успешной интеграции в САПР.

Список литературы

1. Форсайт Д., Понс Ж. Компьютерное зрение. Современный подход.: Пер. с англ. � Москва: Издательский дом �Вильямс�, 2004.-928 с.

2. Москаленко С.В., Гатчин Ю.А., Помехоустойчивый волновой алгоритм векторизации линейных растровых объектов. // Вестник компьютерных и информационных технологий � М., �Машиностроение�. Вып. 5, 2009

3. Feng Su, Jiqiang Song, Shijie Cai: A Vectorization System for Architecture Engineering Drawings.GREC 2005: pp.11-22

4. Karl Tombre, Analysis of Engineering Drawings: State of the Art and Challenges, Selected Papers from the Second International Workshop on Graphics Recognition, Algorithms and Systems, p.257-264, August 22-23, 1997

5. Dori D., Liu W., and Peleg M.: How to Win a Dashed Line Detection Contest. In: Graphics Recognition: Methods and Applications, Lecture Notes in Computer Science, volume 1072, Springer (1996).

6. Bresenham, J.E.: Algorythm for Computer Control and Digtal Plotter. IBM Syst. J. Vol. 4, No.1, April (1965) 25-30

                                                                                                                                                                                    go to published works page ->