|
1РАЗРАБОТКА СИСТЕМЫ АВТОМАТИЧЕСКОЙ ВЕКТОРИЗАЦИИ ЧЕРТЕЖЕЙ
С.В. Москаленко
Научный руководитель д.т.н., профессор Ю.А.
Гатчин
Системный анализ, математическое моделирование и
управление в технических системах
В данной статье рассмотрен
перевод вводимого растрового изображения в векторный формат,
разработка экспорта в формат
DXF.
Преобразование изображения к векторному виду даст
возможность редактирования и манипулирования распознанных
объектов.
Введение
На данный момент существует несколько алгоритмов
автоматической трассировки растра. Например,
CorelTrace Centerline, CorelTrace Advanced Outline
идут в составе пакета Corel Draw 12.
Третий AutoTrace Outline
является алгоритмом трассировки программы
AutoTrace. Был проведен ряд тестов данных алгоритмов
по основным характеристикам: 1. Скорость работы. 2. Процент
потери элементов входного чертежа. 3. Процент искажения от
первоначального изображения. 4. Целостность распознанных
элементов. 5. Эффективность кодирования примитивов. 6.
Наличие функции восстановления искажений. 7.Соответствие
типов линий (входных - выходных). Тестирование выявило
недостаточную надежность данных алгоритмов с точки зрения
выходных характеристик.
В статье разработана система, которая обладает лучшими
выходными параметрами за счет оптимизации основного
алгоритма. Происходит отсеивание лишней информации, при
сохранении информативных данных для последующей векторизации
с распознаванием образов.
Основная часть
Разработанный алгоритм обеспечивает преобразование растровых
изображений в векторный формат, организуя векторы примитивов
в фигуры, вследствие чего облегчается манипулирование этими
фигурами. То есть реализация данного алгоритма станет весьма
полезным инструментом для чертежников, конструкторов,
инженеров, работающих с чертежами, так как с переходом к
векторному формату (вместе с распознаванием образов)
упростятся многие рутинные операции. После параметризации
входного изображения необходимо еще и объединять полученные
вектора в группы по какомулибо критерию. Это и является
главной задачей распознавания: по параметрам векторов
отнести их к конкретной целевой группе.
Основные понятия
Под бинарным растровым изображением будем понимать двумерную
матрицу из черных и белых точек, в которой объект задается
черными точками растра, а фон белыми точками. Первым делом
после ввода изображения, запускается побитовое сканирование
этого изображения на наличие черных точек растра. Вообше,
для описания работы алгоритма необходим ввод понятий: группа,
полилиния, вектор. Вектором называется отрезок, заданный
двумя точками и обладающий следующими атрибутами: координаты
своего начала и конца, тип линии, ссылкой на другой вектор (если
полилиния), и набором геометрических констант необходимых
для распознавания. Полилиния множество последовательно
связанных векторов: любой вектор полилинии имеет два конца,
каждый из которых может иметь одну и только одну общую точку
с другим вектором данной полилинии. Каждая полилиния
обладает началом и концом, а так же состоит как минимум из
двух векторов (рис. 1 (1)). Стыки векторов в полилиниях
узлы.
Группой является любой примитив (полилиния, вектор) либо
любая совокупность полилиний и векторов имеющих общие
концевые точки (рис. 1 (2)). Полилиния, изображенная на рис.
1(1), также является группой. Ветвлением называется случай,
когда концевая точка примитива имеет более одной связи с
другими примитивами (рис. 1 (2)) .
Логично предположить, что для реализации распознавания фигур,
необходимо сначала выявить группы на изображении, а уже
потом анализировать различные комбинации примитивов внутри
каждой группы на предмет принадлежности их какой-либо фигуре.
Это решение намного повысит скорость распознавания, нежели
применение анализа комбинаций всех примитивов внутри всей
генеральной совокупности.

1 полилиния состоящая из трех векторов; 2 - группа
состоящая из двух полилиний и одного вектора
Рисунок 1. Примеры объектов
Образование групп. Работа с тонкими линиями
При обнаружении черного пиксела (далее точки), происходит
проверка окрестности данной точки на наличие соседних черных
точек, предварительно изменив значение данного пикселя в
буфере на 255, что равносильно окрашиванию в белый цвет.
Таким образом, как показано на рис. 2, проверяется 8
соседних пикселей на «черность».
Существует в алгоритме запись mask,
содержащая 8 полей булевого типа. Эта запись необходима для
запоминания расположения соседних точек относительно
рассматриваемой. Во время обнаружения соседних черных
пикселов происходит присваивание соответствующим полям
значения 1. Например, при окрестности соответствующей рис.
2, в полях записи mask будут
храниться следующие значения: 00010100. Таким образом, поля
записи mask образуют маску
окрестности.

Рисунок 2. Пример рассматриваемой окрестности
Если в окрестности обнаружена только одна точка, то
происходит повторный рекурсивный запуск сканирования
окрестности уже с координатами новой точки. Так будет
происходить до тех пор, пока в окрестности не окажется ни
одного черного пиксела.
Если в окрестности обнаружено две точки, это означает, что
встретилось ветвление, и что рассматриваемая точка является
концевой точкой примитива (рис. 3). То есть маска
окрестности, имеющая более одной точки, сигнализирует о
конце данной ветви, плюс происходит операция образования
новой ветви. При переходе рекурсии на новую ветвь происходит
присваивание ей номера, большего на 1 по сравнению с
предыдущей ветвью.

Рисунок 3. Примеры ветвлений
На рис. 4 приведен пример
нумерации ветвей, эта нумерация необходима для дальнейшего
процесса распознавания. Требуется заметить, что каждая ветвь
будет являться примитивом (вектором, полилинией).
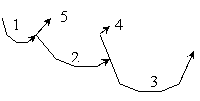
Рисунок 4. Пример нумерации ветвей
Однако, существует ряд исключительных ситуаций, когда при
обнаружении в окрестности двух точек просходит неверная
идентификация ветвей. Первая ситуация двойка изоражена на
рис. 5(1), из которого видно, что дана всего лишь одна ветвь,
однако при анализе окрестности найдено две точки. Чтобы
предотвратить разбиение ветви на подветви, происходит
удаление текущей точки из буфера (окрашивание в белый цвет),
а затем сдвиг на угловую точку исключая операцию образования
нового примитива (рис. 5(2)).
Вторая ситуация угол показана на риc.
5(3). При ее возникновении первичное разбение на примитивы
происходит верно; проходит операция образования нового
примитива, однако, при просмотре окрестности начальной точки
данного примитива выявляется соседство с двумя точками, как
показано на рис. 5(4), что приводит к дроблению нового
примитива на подветви. Для предотвращения ситуации «угол»
идет коррекция соответствующей маски окрестности.
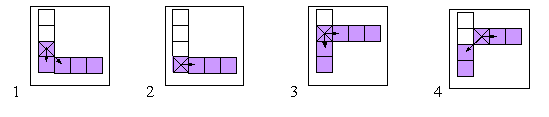
1-
первая итерация ситуации «двойка»; 2 вторая
итерация в «двойке»
2-
первая итерация ситуации «угол»; 4- вторая итерация
в «угле»
Рисунок 5. Примеры исключительных ситуаций
Среди ситуаций, когда в окрестности можно обнаружить более
двух точек, нужно выделить две, рассмотрение которых
исключит все остальные возможные. Ситуация «Тройки» показана
на рис. 6(1), когда в окрестности пиксела обнаружено 3
соседние точки, лежащие в направлениях 1,2,3, или 3,4,5, или
5,6,7, или 7,8,1 от текущей точки (см. рис. 2). Проблемы,
возникающие при выделении примитивов, аналогичны проблемам в
ситуации «угол»: обнаружив «тройки», программа осуществляет
операцию создания нового примитива; при сканировании
окрестности первого пиксела этого примитива в окрестность
попадают «лишние» точки (рисунок 6(2)), которые приводят к
дроблению полученной ветви на подветви. Эта проблема
решается за счет использования специальной процедуры, в
которой происходит задание масок окрестности, исключающих «лишние»
точки.
Вторая ситуация «Кубы» показана на рисунке 6(3), когда в
окрестности пиксела обнаружено 3 соседние точки, лежащие в
направлениях 2,3,4, или 4,5,6, или 6,7,8, или 8,1,2 от
текущей точки (см. рис. 2). В этом случае происходит запуск
еще одной рекурсивной функции для кубов, отслеживающей все
соседние кубы. В этом случае формирование текущего примитива
заканчивается.
Действительно, решения
ситуаций, описанные выше, дадут в результате корректную
организацию ветвлений тонких линий.

1. первая итерация ситуации «тройка»; 2 вторая итерация в
«тройке»;
3
ситуация «куб»
Рисунок 6. Примеры исключительных ситуаций
Работа с
основными линиями
При обнаружении на входном изображении «куба» во время
поиска групп, либо во время выполнения рекурсии тонкой линии,
происходит запуск еще одной рекурсивной функции
отслеживающей все соседние кубы. Последовательность из таких
кубов является ни чем иным, как отображением основной линии.
К основной линии могут быть применены все понятия, связанные
с тонкой линей. Также как и в случае с тонкой линией,
основная линия может содержать ветвления, и также будет
состоять из примитивов. Единственная разница между этими
линями будет в том, что их вектора будут иметь разные
значения атрибута «тип линии».
При обнаружении первого куба, происходит запуск операции
создания нового примитива. Также будет происходить
сканирование окрестности куба и задаваться маска окрестности.
Маска окрестности имеет 16 полей т.е. куб может иметь 16
соседей (рис. 7).
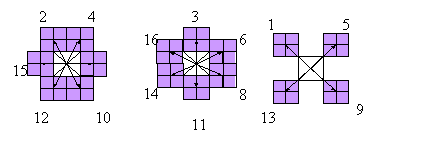
Рисунок 7. Номера направлений соседей для маски окрестности
куба
При сканировании окрестности куба, существует ряд
оптимизационных мер. Например, при обнаружении соседнего
куба в одном из четырех направлений: 3,7,11,15 (рис. 7)
проверка соответствующих пар кубов 2-4, 6-8, 10-12, 14-16 на
их присутствие в окрестности - опускается.
Ход рекурсии при трассировке основных линий аналогичен
рекурсии тонкой линии. Сначала удаляются из буфера 4 пикселя,
задающие данный куб, затем анализируется окрестность
текущего куба, задается маска окрестности. Далее происходит
повторный вызов текущей функции уже с новыми координатами
куба, которые были выбраны согласно маске окрестности. При
нахождении в окрестности более одного куба идет запуск
операции создания нового примитива. Рекурсия будет идти
далее по этому новому примитиву и по всем ответвлениям от
него (если таковые имеются) до тех пор, пока не будут
идентифицированы все его подветви, и после этого происходит
переход на смежный примитив, который имеет общий начальный
куб с начальным кубом данного, уже рассмотренного, примитива.
Это полезное свойство рекурсии позволяет просматривать все
ветви и подветви графа, используя при этом минимум
программного кода.
На рис. 8 приведены различные виды ветвлений.
Еще существует в этой функции проверка наличия соседних
кубов в направлениях 3,5,7, либо в направлениях 7,9,11, либо
в 11,13,5, либо в 15,1,3. Если в каком-либо из четырех
случаев совпали сразу все три направления (этот случай
назван «обширной зоной») происходит вызов соответствующей
процедуры для выделения и обработки обширных зон. Вообще,
такие зоны это области на изображении, состоящие из
большого количества связанных между собой кубов, встречаются
довольно редко, например конец стрелы выносной линии в
большинстве случаев является именно такой зоной.
Естественно, что такие зоны могут вызывать ненужную
избыточность при работе данного алгоритма, то есть почти
каждый куб внутри такой зоны будет иметь по соседу в каждом
из 16 направлений, что приведет к созданию множества
ответвлений из рассматриваемого куба. Для предотвращения
этого, существует специальная процедура, которая удаляет все
кубы этой области из буфера и создает новый примитив с
атрибутом «обширная зона». Этот примитив будет хранить
координаты всех точек этой области и впоследствии будет
использован для распознавания.
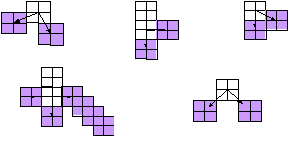
Рисунок 8. Примеры ветвлений основной линии
Ответвления от кубов
Ответвлением называется
случай, когда из основной линии исходит тонкая. Такая
ситуация может возникнуть при пересечении основной линии
тонкой. Ввод понятия «ответвление» необходим для корректной
идентификации группы на входном чертеже, ведь если не будут
учитываться все исходящие тонкие линии (начальные координаты
которых совпадают с координатами основной линии), группа
будет образована неверно, «развалившись» на подгруппы. Это
показано на рис. 9, где целая группа, состоящая из
нескольких примитивов, идентифицировалась как три
обособленных группы каждая группа помечена разным узором.
Исходя из этого следует, что окрестность каждого куба
основной линии должна просматриваться и на наличие
прилегающих пикселей.

Рисунок 9. Пример группы развалившейся на 3 подгруппы
Помимо идентификации ответвлений требуется организовать
алгоритм минимизации, который очищал бы входное изображение
от лишней информации. Например, часто случается, что
изображение основной линии имеет в своей окрестности лишние
точки как оказано на рис. 10. Исключение таких точек
нисколько не понизит информативность изображения. Однако не
стоит забывать и об ответвлениях, ведь при исключении лишних
точек требуется оставить точки начала ответвлений. Точки
начала ответвлений выделены белым цветом на рис. 10 (1).
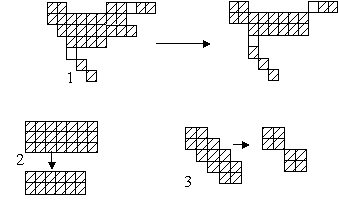
Рисунок 10. Пример работы алгоритма минимизации
Процедура минимизации вызывается всякий раз, когда
происходит переход рекурсии, проверяющей кубы, на новый куб.
При анализе окрестности происходит удаление из буфера лишних
точек («окрашивание в белый цвет») и формирование массива,
содержащего точки начала ответвлений. Когда данная рекурсия
закончит свою работу т.е. найдет все кубы в данной
последовательности, произойдет последовательная выборка
координат всех точек из массива. После чего идет запуск
процедуры идентификации тонкой линии (см. выше) с этими
координатами для каждой точки в отдельности.
Для трех остальных граней применяется та же схема с
соответствующими поворотами. Однако, известна маска
окрестности данного куба, что позволяет применять данный
алгоритм только для необходимых граней. Например, если
найден куб в направлении 7 (см. рис. 7), то к правой грани
данного куба этот алгоритм применен не будет. Если же
обнаружены кубы в направлениях 3,7,11,15, то вызов
минимизационной процедуры для данного куба игнорируется.
После завершения рекурсии основной линии (когда все
связанные кубы обнаружены), происходит извлечение координат
точек начала ответвлений из массива. Далее, происходит вызов
процедуры рукурсии тонкой линии (см. выше) с параметрами
парой координат точки ответвления. Это мероприятие сохранит
целостность групп. Примеры групп на рис. 11.
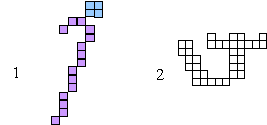
Рисунок 11. Примеры групп
Векторизация примитивов
Для начала рассмотрим векторизацию тонких линий. Как уже
было сказано выше, рекурсия, проходя по последовательности
пикселей, формирует массив координат всех пикселей,
принадлежащих данному примитиву. Формирование примитива
тонкой линии закончено в трех случаях: 1. В окрестности
пиксела не обнаружено ни одной соседней точки. 2. обнаружено
ветвление. 3. Обнаружен переход на основную линию (встреча
куба).
После встречи одной из этих трех ситуаций происходит вызов
процедуры параметризации данного примитива. На данный момент
программа будет обладать массивом точек, которые необходимо
представить в виде последовательности векторов, т.е.
аппроксимировать. Возникают сразу два вопроса: о выборе
точности аппроксимации и о выборе метода аппроксимации.
Для решения проблемы векторизации были взяты основы
алгоритма Брезенхема. Алгоритм генерирует 8-ми связную
развертку отрезка, заданного координатами концов (x1 , y1 ),
(x2 , y2 ). Свойство 8-ми связности представления, допускает
изменения сразу обеих координат (и вертикальной, и
горизонтальной) текущей точки, но не более чем на единицу.
Для решения проблемы векторизации, сначала необходимо
загрузить в буфер первоначальное монохромное изображение.
Далее, имея координаты начальной и конечной точки примитива,
построим отрезок, соединив эти две точки по алгоритму
Брезенхема рис. 12, где левой косой штриховкой выделен
примитив, а правой косой штриховкой выделен отрезок,
соединяющий его концы по Брезенхему.

Рисунок 12. Пример генерации отрезка
алгоритмом Брезенхема.
Во время процедуры генерации данного отрезка, происходит
следующее: процедура, сгенерировав очередной пиксель,
проверяет наличие его в буфере изображения, т.е. если по
координатам данного пикселя в буфере находится черная точка,
это говорит о попадании, и счетчик увеличивается на 1. Под
конец выполнения этой процедуры имеем следующее: длина
сгенерированного отрезка (в пикселях), количество совпадений
точек данного отрезка с точками примитива. Вычислив
отношение этих двух величин, программа получит процент
успеха аппроксимации, т.е. точности. В данной программе был
выбран порог точности 85%. Этот процент наиболее удачен с
точки зрения приближенности к входному изображению (минимум
искажений) и с точки зрения эффективности кодирования
примитива. Под эффективностью кодирования понимается
количество векторов, затраченных на описание данного
примитива.
Многие примитивы, будут состоять из нескольких векторов (например,
дуга), и чтобы аппроксимировать их, одной итерации процедуры
соединения отрезка недостаточно. Для решения этой проблемы,
в программе организован цикл, который соединяет концы
примитива и проверяет точность аппроксимации. Если точность
оказывается меньше 85%, тогда совокупность точек этого
примитива делится пополам, соединяются концы полученного
подпримитива. Если точность снова оказывается
неудовлетворительной, тогда деление идет повторно. И так до
тех пор, пока программа не получит требуемую точность (рис.
13(а)). При получении требуемой точности, на рассмотрение
берется следующий примитив, начало которого совпадает с
концом только что параметризованного подпримитива, а конец
с концом входного примитива (рис. 13(б)). Для полученного
подпримитива снова проходит цикл аппроксимации. В итоге
получаем разбитый примитив в виде совокупности векторов.

а - пример векторизации первого; б - векторизация второго
подпримитива
Рисунок 13. Примеры разбиения на вектора (цифры на рисунках
номера итераций приближения)
В данной работе метод Брезенхема дополнен рядом
усовершенствований для более эффективной векторизации. Так,
например, объект, изображенный на рис. 14(1), данный
алгоритм распознал бы как совокупность нескольких векторов -
что не эффективно с точки зрения кодирования примитивов.
После модификации данный метод задаст объект, изображенный
на рис. 14(1), всего лишь одним вектором (рис. 14(2)).

Рисунок 14. Пример векторизации
Если при аппроксимации примитива выяснилось, что он состоит
нескольких векторов, т.е. является полилинией, тогда при
задании атрибутов каждого вектора задается ссылка на
следующий вектор данной полилинии.
При аппроксимации основных линий используются те же самые
принципы, описанные выше. Каждый куб задается координатами
единственного пиксела, расположенного в левом нижем углу
данного куба, формируется массив из этих пикселей, и далее с
этим массивом будут работать все процедуры, работавшие с
векторизацией тонких линий.
Заключение
В данной статье реализован алгоритм перевода вводимого
растрового изображения в векторный формат непосредственно с
распознаванием образов, который обладает высокими выходными
параметрами: 1. Скорость работы. 2. Процент потери элементов
входного чертежа. 3. Процент искажения от первоначального
изображения. 4. Целостность распознанных элементов. 5.
Эффективность кодирования примитивов. 6. Наличие функции
восстановления искажений. 7.Соответствие типов линий (входных
- выходных).
Преобразование изображения к векторному виду дает
возможность редактирования и манипулирования распознанных
объектов.
Литература
1. Анисимов Б. В., Курганов
В.Д, Злобин В.К. Распознавание и цифровая обработка
изображений: Учеб. пособие для студентов вузов. М.: Высш.
шк., 1983. 295 с. ил.
2. Горелик А.Л., Скрипкин
В.А. Методы распознавания: Учеб. пособие. 2-е изд.,
перераб. и доп. М.: Высш.шк., 1984. 208 с., ил.
3. Дуда Р., Харт П.
Распознавание образов и анализ сцен - М.: Мир, 1976.
4. Прэтт У. Цифровая
обработка изображений (в 2-х книгах) - М.: Мир, 1982.
5. Ту Дж., Гонсалес Р.
Принципы распознавания образов - М.: Мир, 1978.
6. Фу К. Последовательные
методы в распознавании образов - М.: Наука, 1971.
7. Фу К. Структурные методы
в распознавании образов - М.: Мир, 1977.
Хант Э. Искусственный
интеллект - М.: Мир, 1978.
8. Барабаш Ю. Л. Учет свойств
признаков при распознавании. Известия АН СССР. Техническая
кибернетика, 1965, №5.
9.
Чечкин А .В . Математическая информатика . -М .: Наука . Гл . ред . физ .
- мат. лит ., 1991.
10. Загоруйко Н .Г .
Прикладные методы анализа данных и знаний . // Новосибирск.
Изд во института математики . 1999.
11. Горелик А .Л ., Гуревич И
.Б ., Скрипкин В .А . Современное состояние проблемы
распознавания . // М .: Радио и связь , 1985, 160 с .
12. Журавлев Ю .И . Об
алгебраическом подходе к решению задач распознавания и
классификации . // Проблемы кибернетики . М .: Наука .
1978.-вып . 33. с .5-68.
13. Гренандер У . Лекции по
теории образов . // М .: Мир , 1979, 1 том ; 1981, 2 том ;
1983, 3 том .
14. Жданов А .А . Об одном
имитационном подходе к адаптивному управлению . Сборник
"Вопросы кибернетики". Научный совет по комплексной проблеме
"Кибернетика"
РАН , Выпуск
2. М
., 1996, С . 171-206.
15. Жданов А. А ., Метод
автономного адаптивного управления . // Известия Академии
Наук .
go to published works page -> |