|
С.В. Москаленко
Санкт-Петербургский
государственный университет информационных технологий
механики и оптики
АЛГОРИТМ ВЕКТОРИЗАЦИИ
ПРИМИТИВОВ БИНАРНЫХ РАСТРОВЫХ ИЗОБРАЖЕНИЙ
Достигнутые
результаты в области цифровых методов представления и сжатия
изображений на сегодняшний день не решают в полной мере
задачу их эффективного представления, что делает поиск
эффективного представления изображений актуальным. Одним из
путей ее решения представляется разработка интеллектуальных
технологий обработки изображений, обеспечивающих не
формализованное их кодирование, а распознавание их
пространственной структуры, которая и является носителем
заключенной в них информации, поскольку возможности
извлечения полезной информации из изображений целиком и
полностью определяется их пространственно-структурными
свойствами.
Задачу распознавания может
состоять из нескольких этапов. Одним из начальных будет
являться этап перехода от растрового изображения к
векторному.
Под бинарным растровым изображением будем понимать двумерную
матрицу из черных и белых точек, в которой объект задается
черными точками растра, а фон ¢ белыми точками. Первым делом
после ввода изображения, запускается побитовое сканирование
этого изображения на наличие черных точек растра. Вообше,
для описания работы алгоритма необходим ввод понятия
примитив, который может быть представлен:
полилинией,
вектором, точкой.
Вектором называется отрезок, заданный двумя точками и
обладающий следующими атрибутами: координаты своего начала и
конца, тип линии, ссылкой на другой вектор (если полилиния),
и набором геометрических констант необходимых для
распознавания. Полилиния ¢ множество последовательно
связанных векторов: любой вектор полилинии имеет два конца,
каждый из которых может иметь одну и только одну общую точку
с другим вектором данной полилинии. Каждая полилиния
обладает началом и концом, а так же состоит как минимум из
двух векторов (рис. 1). Стыки векторов в полилиниях ¢ узлы.
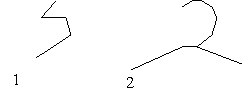
Рисунок 1 Примеры групп
1 ¢ полилиния
состоящая из трех векторов; 2 - группа состоящая из двух
полилиний и одного вектора.
При растровом представлении
каждый примитив будет задан поточечно, то есть алгоритм
будет обладать массивом координат точек. Далее этот массив
точек необходимо преобразовать к последовательности векторов,
т.е. аппроксимировать. Возникают сразу два вопроса: о выборе
точности аппроксимации и о выборе метода аппроксимации.
Для решения проблемы векторизации были взяты основы алгоритма
Брезенхема. Алгоритм генерирует 8-ми связную развертку
отрезка, заданного координатами концов (x1 , y1 ), (x2 , y2
). Свойство 8-ми связности представления, допускает
изменения сразу обеих координат (и вертикальной, и
горизонтальной) текущей точки, но не более чем на единицу.
Для решения
проблемы векторизации, сначала необходимо загрузить в буфер
первоначальное
растровое бинарное
изображение. Далее,
имея координаты начальной и конечной точки примитива,
алгоритм строит
отрезок, соединяя
эти две точки по алгоритму Брезенхема ¢ рис. 2, где левой
косой штриховкой выделен примитив, а правой косой штриховкой
выделен отрезок, соединяющий его концы по Брезенхему.

Рисунок 2 Пример генерации отрезка
(алгоритм
Брезенхема)
Во
время процедуры генерации данного отрезка, происходит
следующее: процедура, сгенерировав очередной пиксель,
проверяет наличие его в буфере изображения, т.е. если по
координатам данного пикселя в буфере находится черная точка,
это говорит о попадании, и счетчик увеличивается на 1. Под
конец выполнения этой процедуры имеем следующее: длина
сгенерированного отрезка (в пикселях), количество совпадений
точек данного отрезка с точками примитива. Вычислив
отношение этих двух величин, программа получит процент
успеха аппроксимации, т.е. точности. В данной программе был
выбран порог точности ¢ 85%. Этот процент наиболее удачен с
точки зрения приближенности к входному изображению (минимум
искажений) и с точки зрения эффективности кодирования
примитива. Под эффективностью кодирования понимается
количество векторов, затраченных на описание данного
примитива.
Примитивы
могут
состоять из нескольких векторов (например, дуга), и чтобы
аппроксимировать их одной итерации процедуры
генерации
отрезка недостаточно. Для решения этой проблемы
организован
цикл, который соединяет концы примитива и проверяет точность
аппроксимации. Если точность оказывается меньше 85%, тогда
совокупность точек этого примитива делится пополам,
соединяются концы полученного подпримитива. Если точность
снова оказывается неудовлетворительной, тогда деление идет
повторно. И так до тех пор, пока программа не получит
требуемую точность (рис. 3(а)). При получении требуемой
точности, на рассмотрение берется следующий примитив, начало
которого совпадает с концом только что параметризованного
подпримитива, а конец ¢ с концом входного примитива (рис.
13(б)). Для полученного подпримитива снова проходит цикл
аппроксимации. В итоге получаем разбитый примитив в виде
совокупности векторов.
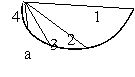 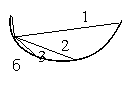
а - пример
векторизации первого;
б - второго
подпримитива
Рисунок 3 Примеры разбиения на вектора (цифры на рисунках ¢
номера итераций приближения).
В алгоритме метод Брезенхема
дополнен рядом усовершенствований для более эффективной
векторизации. Так, например, объект, изображенный на рис.
4(1), данный алгоритм распознал бы как совокупность
нескольких векторов - что не эффективно с точки зрения
кодирования примитивов. После модификации данный метод
задаст объект, изображенный на рис. 4(1), всего лишь одним
вектором (рис. 4).

Рисунок 4. Пример
векторизации
Если при аппроксимации примитива выяснилось, что он состоит нескольких
векторов, т.е. является полилинией, тогда при задании
атрибутов каждого вектора задается ссылка на следующий
вектор данной полилинии.
В результате работы
алгоритма получаем массив векторов, обладающих следующими
атрибутами: координаты начала, конца, ссылки на смежные (имеющие
общий узел с данным вектором) вектора.
Разработанный
алгоритм, предназначенный
для обработки и
отображения графических данных,
обладает
повышенной
эффективностью,
причем под эффективностью понимается не только повышение
быстродействия алгоритма, но и улучшение качества
получаемого решения.
Библиографический
список
1. Анисимов Б. В., Курганов В.Д, Злобин В.К. Распознавание и цифровая
обработка изображений: Учеб. пособие для студентов вузов. ¢
М.: Высш. шк., 1983. ¢ 295 с. ил.
2. Горелик А.Л., Скрипкин В.А. Методы распознавания: Учеб. пособие. ¢
2-е изд., перераб. и доп. ¢ М.: Высш.шк., 1984. ¢ 208 с.,
ил.
3. Дуда Р., Харт П. Распознавание образов и анализ сцен - М.: Мир,
1976.
4. Прэтт У. Цифровая обработка изображений (в 2-х книгах) - М.: Мир,
1982.
5. Ту Дж., Гонсалес Р. Принципы распознавания образов - М.: Мир, 1978.
6. Фу К. Последовательные методы в распознавании образов - М.: Наука,
1971.
7. Фу К. Структурные методы в распознавании образов - М.: Мир, 1977.
Хант Э.
Искусственный интеллект - М.: Мир, 1978.
8. Барабаш Ю. Л.
Учет свойств признаков при распознавании. ¢ Известия АН
СССР. Техническая кибернетика, 1965, №5.
9. Чечкин А .В . Математическая информатика . -М .: Наука .
Гл . ред . физ . - мат. лит ., 1991.
10. Загоруйко Н .Г .
Прикладные методы анализа данных и знаний . // Новосибирск.
Изд ¢во института математики . 1999.
11. Горелик А .Л .,
Гуревич И .Б ., Скрипкин В .А . Современное состояние
проблемы распознавания . // М .: Радио и связь , 1985, 160 с
.
12. Журавлев Ю .И . Об
алгебраическом подходе к решению задач распознавания и
классификации . // Проблемы кибернетики . М .: Наука .
1978.-вып . 33. с .5-68.
13. Гренандер У .
Лекции по теории образов . // М .: Мир , 1979, 1 том ; 1981,
2 том ; 1983, 3 том .
14. Жданов А .А . Об
одном имитационном подходе к адаптивному управлению .
Сборник "Вопросы кибернетики". Научный совет по комплексной
проблеме "Кибернетика"
РАН , Выпуск
2. М
., 1996, С . 171-206.
15. Жданов А . А .,
Метод автономного адаптивного управления . // Известия
Академии Наук ..
go to published works page -> |