|
УДК 004.932
½ПОМЕХОУСТОЙЧИВЫЙ ВОЛНОВОЙ АЛГОРИТМ ВЕКТОРИЗАЦИИ ЛИНЕЙНЫХ
РАСТРОВЫХ ОБЪЕКТОВ╗
½NOISE STABLE WAVE METHOD FOR RASTER LINE VECTORIZATION╗
С.В. Москаленко, Ю.А. Гатчин ¢ д.т.н.
Санкт-Петербургский государственный
университет информационных технологий, механики и оптики, г.
Санкт-Петербург.
Рассмотрено новое решение
проблемы векторизации линейных бинарных растровых объектов,
обладающее повышенной эффективностью. Под эффективностью
понимается низкая
трудоемкость и высокое качество результатов обработки,
помехоустойчивость,
которая обусловлена использованием генераций сферических
волн для нахождения центральных линий растровых объектов.
A new approach
for the crude vectorization of binary images is considered.
The approach has high efficient capabilities such as low
time complexities, shape preservation,
robustness to
various noise types at reasonable levels. These capabilities
are defined using the circular waves generations to detect
raster object centerlines.
Ключевые слова: векторизация, скелетизация,
центральная линия, сегментация, связность.
Keywords:
vectorization, skeletonization, centerline, segmentation,
connectivity.
Введение
Общая задача векторизации сводится к процессу обнаружения
линейных примитивов на растровых изображениях. Он является
предобработкой для распознавания объектов более высокого
уровня (печатных символов, картографических объектов
геоинформационных систем, графических объектов медицинских
снимков), которую можно подразделить на два основных этапа.
На первом этапе выполняют первичную векторизацию,
разбивают пиксели растра на группы примитивов:
l
точка,
l
отрезок,
l
полилиния,
l
площадной объект.
Каждый примитив должен наиболее точно отражать топологию
соответствующего объекта на растровом изображении, а так же
иметь набор атрибутов:
l
ширина линии (в случае отрезка, полилинии),
l
набор характерных точек,
l
связи с другими объектами.
Данный этап является предметом исследования в областях
анализа и распознавания изображений уже многие годы. Не
смотря на это, анализ существующих решений выявил
недостаточную их надежность с точки зрения выходных
характеристик: быстродействия, уровня сохранения
топологической связности с исходным изображением.
На втором этапе происходит объектная векторизация,
когда множества примитивов, полученных на предыдущем этапе,
проверяются на принадлежность заданным классам объектов.
Задача первичной векторизации распадается на несколько
подзадач, первая из которых ¢ сегментация. Под
сегментацией подразумевается определение типа объекта:
l
текст или графика,
l
площадной объект или линейный,
l
разделение на тонкие или толстые линии.
Следующая подзадача ¢ параметризация, служащая
выявить топологию объектов с сохранением необходимых
атрибутов. Во время параметризации происходит выделение
средних линий объектов в виде цепочек пикселей растра.
Завершает этап первичной векторизации подзадача линейной
аппроксимации найденных осевых линий, в результате
которой формируется модель изображения в виде набора
отрезков и полилиний. Эта подзадача является достаточно
проработанной в литературе [1], поэтому в данной статье этап
первичной векторизации ограничен лишь описанием подзадач
сегментации и параметризации.
В статье проведен анализ существующих решений этапа
первичной векторизации, на основании которого предложено
новое решение, обладающее лучшими выходными параметрами за
счет оптимизации основного алгоритма.
Обзор существующих подходов
Многие методы этапа первичной векторизации были разработаны
и реализованы более тридцати лет назад. Эти методы можно
разделить на шесть классов [2], основанных на различных
методах:
l
преобразовании Хафа;
l
утоньшении линий;
l
сопоставлении контуров;
l
графах бегущих штрихов;
l
разбиении изображения регулярной сеткой;
l
разреженном просмотре растра.
Сравнительный анализ данных алгоритмов выявил, что только
методы, основанные на разбиении изображения регулярной
сеткой, а также методы, основанные на разреженном просмотре
растра, обладают линейной сложностью по отношению к
разрешению растра, в то время как остальные имеют кубические
и квадратичные сложности. Также только с помощью методов,
основанных на разреженном просмотре растра [3, 4], получают
объекты, обладающие высокой степенью соответствия исходной
топологии, сохраняют ширину линейных объектов и имеют
функцию восстановления связности в узлах.
Связность - довольно важная характеристика работы этапа
первичной векторизации так как сохранение связей между
объектами упрощает задачу анализа изображения на более
высоких уровнях. Сохранение связей обеспечивается
восстановлением разрывов между линейными объектами путем их
объединения в один объект. Разрывы бывают естественные,
например, в случае штрихпунктирных линий, и фиктивные,
которые могут быть образованы шумами на растре или
некорректной работой алгоритма.
Так алгоритм Sparce Pixel Vectorization
(SPV), показавший наилучший
результат векторизации среди методов распределенного
анализа, завершает процедуру сбора точек средней линии при
смене направления отслеживания, например с вертикального на
горизонтальное, что ведет к разрыву линейного объекта [4].
Также выборочный анализ растра обуславливает возможность
пропуска ответвлений от объекта, что также ведет к разрыву.
На рис. 1 проиллюстрирована работа процедуры отслеживания
центральной линии для такого случая. Шаг работы данной
процедуры характеризуется проверкой длин вертикального и
горизонтального пробега, при превышении длины любого из
которых, делается вывод о возможном ответвлении. Однако шаг
процедуры отслеживания может пропустить изменение ширины
линии, как показано на рис. 1, а, тогда
рассматриваемый растровый объект будет удален в ходе
редукции данных. В результате получаем разрыв, показанный на
рисунке 1, б.
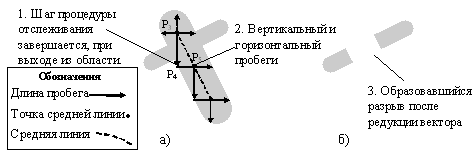
Рис. 1. Процедура отслеживания центральной линии алгоритма
SPV
Еще одним недостатком работы алгоритма
SPV является наличие возможности ошибочного
определения начальной вершины вектора, что исказит векторную
модель относительно исходной топологии. Вершина вектора
может оказаться смещенной, т. е. данный примитив будет
укорочен. Пример ошибочного вычисления показан на рис. 2.
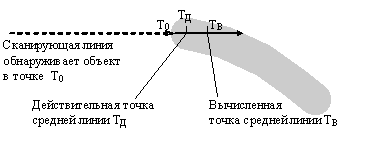
Рис. 2. Вычисление
начальной вершины вектора алгоритма SPV
Существуют подходы, которые для обеспечения связности
тщательно контролируют изменение толщины линии. Происходит
расчет средней линии, одновременно с анализом контура [5].
При получении координат точки запускается процесс, состоящий
из следующих этапов:
l
центрирование точки указания;
l
определение направления (путем построения
циклической гистограммы);
l
вычисление точек центральной линии.
После определения предпочтительных направлений производится
замер толщин (ширина линии в пикселях) в направлениях
перпендикулярных двум базовым, одновременно с этим
происходит процесс вычисления точек центральной линии в
обоих направлениях с шагом в одну растровую точку. Процесс
замера толщин отслеживает резкое изменение толщины линии,
что говорит о наличии ветвления (пересечения) в данной
области. При обнаружении вышеописанной ситуации процесс
останавливается в данном направлении и начинается в
противоположном. Однако попиксельный расчет толщин является
весьма трудоемкой операцией.
Для работы большинства алгоритмов векторизации необходимо
содействие пользователя в выборе определенных констант:
максимальной ширины линии, допустимой длины пробега (в
случае SPV), что лишает систему
автоматического режима работы.
Реализация алгоритма
В разработанном алгоритме векторизации отсутствует как
попиксельное вычисление толщины линии, так и этап
определения предпочтительных направлений.
-
После ввода бинарного
изображения запускают побитовое сканирование этого
изображения на наличие ½черных╗ точек растра
c интервалом в 10 пикселей.
-
От полученной исходной точки в
основных направлениях строят циклическую гистограмму по
черным пикселям до первого белого. С помощью нее
определяют ширину линейного объекта и тип обнаруженной
области. В связи с ограниченным числом лучей циклической
гистограммы, выходящих из исходной точки, длина участка
пересечения лучом графического объекта может отличаться
от реальной толщины объекта в данной точке. Ошибку
вычисления толщины для такого случая определяют по
формуле (1):
Δ
= 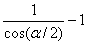 ,
(1) ,
(1)
где α ¢ угол между смежными лучами.
Число лучей гистограммы было взято равным 36, так как при α
= 10 градусов ошибка вычисления толщины объекта не превысит
1,5%.
Для вычисления координат точек при построении гистограммы
использовантиповой алгоритм Брезенхема (генерации отрезка).
В результате могут получиться гистограммы с ярко
выраженными пиками или неопределенные.
Под ярко выраженным пиком понимается участок на графике,
когда функция резко возрастает в один момент и сразу
убывает. При чем высота пика должна быть больше ширины
линейного объекта в 2 раза. Так, например, если график будет
иметь один или два пика, это будет говорить о том, что
исходная точка принадлежит отрезку или дуге, т. е. линейному
примитиву (рис. 3, а). Если на функции обнаружатся более
двух пиков, значит исходная точка лежит на пересечении
линейных объектов (рис. 3, б). Неопределенной будем считать
ту гистограмму, которая имеет неопределенные пики (рис. 3,
в). Такие пики есть отображение площадных объектов на
растре. Проанализировав функции, можно отнести существующие
объекты растрового изображения либо к площадным, либо к
линейным.
3. После построения гистограммы определяют толщину отрезка (для
линейных объектов). Если найдено только два явных пика, то
можно сделать вывод, что исходная точка достаточно удалена
от обеих вершин линейного объекта. Если пик один, то точка
примерно совпадает с одной из вершин. Для случая обнаружения
двух явных пиков должно быть вычислено среднее значение
величин на гистограмме, лежащих в непосредственной близости
от точки экстремума, принадлежащей участку функции между
двумя вершинами пиков (только одна точка экстремума может
быть найдена). Полученное значение будет отражать толщину
линии (рис. 3, а).
Для случая одного явного пика должно быть вычислено среднее
значение величин, лежащих в окрестности точки перехода от
выпуклого участка функции к вогнутому (или прямолинейному),
которая может находиться как слева, так и справа от вершины
пика. Полученное значение также будет отражать толщину линии
(рис. 3, г).
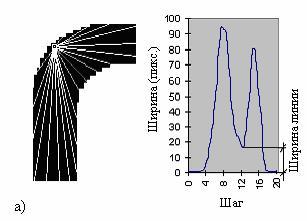 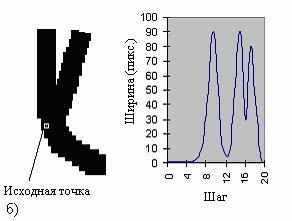
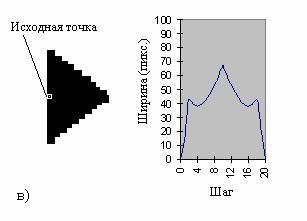 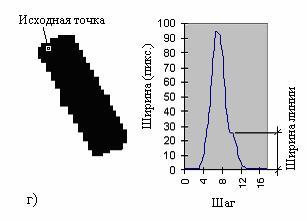
Рис. 3. Примеры гистограмм растровых изображений
(слева растровое изображение, справа гистограмма): а
¢ дуга; б ¢ исходная точка лежит на пересечении; в
¢ площадной объект; г - исходная точка совпадает с
вершиной прямой.
Проанализировав гистограмму, определим толщину линии,
координаты двух концов поперечного сечения и исходной точки.
Теперь можно найти точку центра масс на данном сечении ¢ это
будет его середина.
Для вычисления точек центральной линии и для проверки на
принадлежность растрового объекта классу линейных объектов,
реализован волновой алгоритм. Суть его заключается в
построении сферической волны, центр которой совпадает с
последним найденным центром масс, а радиус равен ширине
растрового объекта в исходной точке. Построение сферической
волны обеспечивает тщательное отслеживание контура, обладая
при этом разреженным анализом растра, что сохраняет
связность как при смене направления отслеживания (случай
SPV-алгоритма), так и при
нахождении ветвления.
Отцентрировав исходную точку на сечении, алгоритм генерирует
окружность радиусом равным толщине линии, используя типовой
алгоритм Брезенхема (генерации окружности). Построенная
окружность должна пересечь границу растрового объекта с
фоном 2n раз в зависимости от
результатов анализа построенной ранее гистограммы. Например,
если сделан вывод, что исходное сечение не совпадает с
вершиной линейного объекта, значит, окружность должна
пересечь границу четыре раза, так как растровый объект будет
развиваться в двух направлениях.
Далее проведем через полученные пары точек две прямые таким
образом, чтобы образовалось два поперечных сечения. Каждая
из середин полученных сечений будет являться новым центром
масс, из которого будет выходить очередная волна.
Итерационное развитие волн в одном направлении будет
продолжаться до тех пор, пока окружность не пересечет
растровый объект в количестве точек не равном двум или
вообще не пересечет растровый объект, либо же пока не
произойдет резкое изменение ширины продольного сечения, что
будет говорить о наличии утоньшения, утолщения или
пересечения (рис. 4). При обнаружении вышеописанной ситуации
процесс останавливается в данном направлении и начинается в
противоположном.
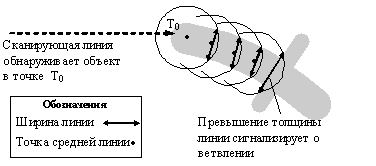
Рис. 4. Вычисление точек средней линии растрового объекта
Таким образом, данный алгоритм позволит получить координаты
точек центральной линии с информацией о ширине линии в
каждой точке. Данные параметры необходимы для векторного
представления растровых объектов.
Что касается генерации самой волны, то во время первой
итерации необходимо строить полную окружность, а для
последующих итераций можно ограничиться лишь разверткой
(9/8)π. Данная развертка должна откладываться по обе стороны
от перпендикуляра, построенного к сечению, которое было
получено в результате предыдущего построения волны.
На рис. 4 проиллюстрирована работа процедуры отслеживания
центральной линии (оси), которая реализуется путем
итерационного воспроизведения генераций волн. Для данного
случая процедура продолжается до тех пор, пока не
встретилось значительное увеличение ширины линейного
объекта. Следует отметить, что даже при высоком уровне
зашумленности изображения (края линейного объекта неровные),
точки центральной линии вычисляются корректно.
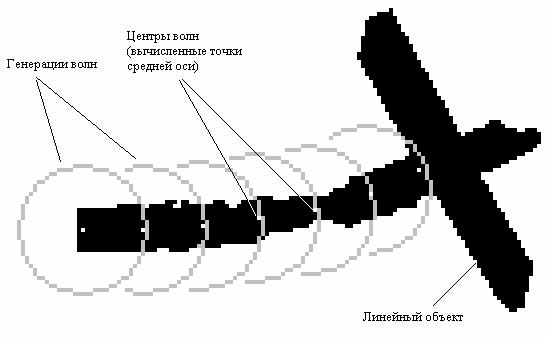
Рис. 5. Вычисление точек средней оси
растрового объекта
Заключение
Разработанный алгоритм, предназначенный для обработки и
отображения графических данных, обладает повышенной
эффективностью, причем под эффективностью понимается не
только повышенное быстродействие алгоритма, но и улучшенное
качество получаемого решения, когда полученная векторная
модель наиболее точно соответствует топологии входного
растра. Эта эффективность обусловлена использованием
генерации сферических волн для нахождения центральных линий
растровых объектов. При разреженном просмотре растра
сохраняется связность. Анализ гистограмм позволяет добиться
автоматической работы алгоритма без вмешательства человека.
Также данный алгоритм показал высокую помехоустойчивость.
Эффективное преобразование изображения к векторному виду
является важным шагом в процессе обработки изображения. От
результатов его работы будут зависеть процедуры анализа
более высокого уровня, такие как распознавание графических
образов для импортирования в САПР. Реализованный алгоритм
обладает всеми необходимыми характеристиками для успешной
реализации в этапах, предшествующих процедурам высокого
уровня.
ЛИТЕРАТУРА
1.
Sklansky
J.,
Gonzalez
V.
Fast
Polygonal Approximation of Digitized Curves // Pattern
Recognition, 1980. Vol.12. P. 327-331.
2. Новиков Ю.Л. Эффективные
алгоритмы векторизации растровых изображений и их реализация
в геоинформационной системе: автореф. дис. канд.
техн. наук. М., 2002 С.20
3.
Dori D., Liu W. Sparse Pixel Vectorization, An Algorithm and
its Performance Evaluation // IEEE Trans. on Pattern
Analysis and Machine Intelligence. 1999. Vol. 21. № 3.
Р. 202¢215.
4.
Dori D. Orthogonal Zig-Zag: An Algorithm for Vectorizing
Engineering Drawings Compared with Hough Transform //
Advances in Software Engineering.1997.
Vol. 28.
№ 1. Р. 11¢24.
5. Крылов А.Б. Способ выбора
растровых объектов на монохромном изображении с
автоматическим вычислением геометрических параметров:
сборник статей ½Интеллектуальные технологии и системы╗
- Моск. гос. техн. ун-т им.
Н.Э.Баумана 2001. Вып.5
С.34-42.
go to published works page ->
|